5.7 Structures

Hydraulic structures in the 1D domain are modelled by replacing the momentum equation with standard equations describing the flow through the structure. The structures available are described in the following sections. A discussion on the choice of a 1D or 2D representation of the structure is presented in Section 7.2.9.1.

A channel is flagged as a hydraulic structure using the Type attribute as described in Table 5.1. Except for culverts, a structure has zero length, i.e. there is no bed resistance. If a non-zero length is applied to a “zero length” structure, this is only used in the calculation of the storage (nodal area).

5.7.1 Culverts and Pipes

Culvert or pipe channels can be either rectangular, circular (pipe) or irregular in shape. A range of different flow regimes is simulated with flow in either direction. Adverse slopes are accounted for and flow may be subcritical or supercritical. Figure 5.4, Figure 5.5 and Table 5.6 present the different flow regimes which can be modelled. The regimes that occur during a simulation are output to the .eof file next to the velocity and flow output values, and to the _TSF GIS layer (see Sections 14.5 and 15.2.4), and can be displayed on time-series plots in the QGIS TUFLOW Viewer plugin.

For all culvert types the length, upstream and downstream inverts, Manning’s n, bend loss, entrance and exit losses, and number of barrels are entered using the 1d_nwk attributes (see Table 5.5). For type “C” circular or type “R” rectangular culverts, the dimensions are also specified within the 1d_nwk attributes. For an “I” irregular shaped culvert, the cross-sectional shape is specified using a 1d_xs GIS layer and the Read GIS Table Links command. The line must be digitised across the 1d_nwk channel line using the mid cross-section approach (refer to Section 5.6.5 and Table 5.4). This is the only supported approach for structures such as irregular shaped culverts, bridges, and weirs.

The four culvert coefficients are as follows:

  • The height contraction coefficient for box culverts. Usually 0.6 for square edged entrances to 0.8 for rounded edges. This factor is not used for circular culverts.
  • The width contraction coefficient for box culverts. Typically values from 0.9 for sharp edges to 1.0 for rounded edges. This factor is normally set to 1.0 for circular culverts.
  • The entry loss coefficient. The standard value for this coefficient is 0.5. Variations to this value may be applied based on manufacturer specifications.
  • The exit loss coefficient, normally recommended as 1.0.

The calculations of culvert flow and losses are carried out using techniques from “Hydraulic Charts for the Selection of Highway Culverts” and “Capacity Charts for the Hydraulic Design of Highway Culverts”, together with additional information provided in Henderson (1966). The calculations have been compared and shown to be consistent with manufacturer’s data provided by both “Rocla” and “Armco”.

Note: By default, the entrance and exit losses above are adjusted every timestep according to the approach and departure velocities based on the equations in Section 5.7.7.

For benchmarking of culvert flow to the literature, see “TUFLOW Validation and Testing” (Huxley, 2004).

Table 5.5: Culverts and Pipes: 1D Model Network (1d_nwk) Attribute Descriptions
No.  Default GIS Attribute Name Description Type
1 ID Unique identifier up to 12 characters in length. It may contain any character except for quotes and commas, and cannot be blank. As a general rule, spaces and special characters (e.g. “\”) should be avoided, although they are accepted. The same ID can be used for a channel and a node, but no two nodes and no two channels can have the same ID.
When automatically creating nodes (default) “.1” and “.2” are added to the channel names for the upstream and downstream node names respectively. IDs over 10 characters long are not recommended as the appending of .1 and .2 can cause duplicate node ID’s to be created. 		Char(12)
2 Type

The culvert type:

  • “C” for a circular culvert;
  • “R” for a rectangular culvert;
  • “I” for an irregular shaped culvert
Optional type flags may also be used to implement additional flow controls such as unidirectional flow (“U”) or operated flow conditions (“O”). Culvert type details are outlined in Table 5.1 and optional flags in Table 5.2 . 		Char(4)
3 Ignore If a “T”, “t”, “Y” or “y” is specified, the object will be ignored (T for True and Y for Yes). Any other entry, including a blank field, will treat the object as active. Char(1)
4 UCS
(Use Channel Storage at nodes) 		If left blank or set to Yes (“Y” or “y”) or True (“T” or “t”), the storage based on the width of the channel over half the channel length is assigned to both of the two nodes connected to the channel. If set to No (“N” or “n”) or False (“F” or “f”), the channel width does not contribute to the node’s storage. See Section 5.12 for further discussion. Char(1)
5 Len_or_ANA The length of the culvert in metres. If the length is less than zero, except for the special values below, the length of the line is used. Float
6 n_nF_Cd

The Manning’s n value of the culvert.

If using materials to define the bed resistance from XZ tables (only for Irregular culvert, see Section 5.6.1.1.2), n_nF_Cd should be set to one (1) as it becomes a multiplication factor of the materials’ Manning’s n values. It may be adjusted as part of the calibration process. 		Float
7 US_Invert

The upstream bed or invert elevation of the culvert in metres.

If a culvert invert has a value of -99999 (after any application of node/pit DS_Invert values), the invert is interpolated by searching upstream and downstream for the nearest specified inverts, and the invert is linearly interpolated. Interpolate Culvert Inverts can also be used to switch this feature ON or OFF. 		Float
8 DS_Invert Sets the downstream invert of the culvert using the same rules as for described for the US_Invert attribute above. Float
9 Form_Loss Specifies an additional dynamic head loss coefficient that is applied when the culvert flow is not critical at the inlet. This applies the energy loss appropriately for a ‘minor’ loss using K*V2/2g. Bend loss coefficients (K) are found in many standard hydraulic references. Note, this loss coefficient is not subject to adjustment when using Structure Losses == ADJUST, and is ideally used to model additional energy losses such as bend losses. Float
10 pBlockage

C, R Channel Type:
The percentage blockage (for 10%, enter 10) of the culvert. For R culverts, the culvert width is reduced by the % Blockage, while for C culverts the pipe diameter is reduced by the square root of the % Blockage. Note that when applying a % Blockage to C culverts, the invert level remains unchanged and only the soffit level is reduced by the calculated decrease in diameter.

I Channel Type:
Not used.

To apply a blockage to irregular shaped structures, see the skew angle attribute within Table 5.4. 		Float
11 Inlet_Type Not used. Char(256)
12 Conn_1D_2D Not used. Char(4)
13 Conn_No Not used. Integer
14 Width_or_Dia

C Channel Type:
The pipe diameter in metres.

R Channel Type:
The box culvert width in metres.

I Channel Type:
Not used. 		Float
15 Height_or_WF

R Channel Type:
The box culvert height in metres.

C, I, Channel Type:
Not used. 		Float
16 Number_of The number of culvert barrels. If set to zero, one barrel is assumed. Integer
17 HConF_or_WC

I, R Channel Type:
The height contraction coefficient for orifice flow at the inlet. Usually 0.6 for square edged entrances to 0.8 for rounded edges. If value exceeds 1.0 or is less than or equal to zero, it is set to 1.0.
Not used for unsubmerged inlet flow conditions or outlet controlled flow regimes.

C Channel Type:
Not used. 		Float
18 WConF_or_WEx

The width contraction coefficient for inlet-controlled flow. Usually 0.9 for sharp edges to 1.0 for rounded edges for R culverts. Normally set to 1.0 for C culverts. If value exceeds 1.0 or is less than or equal to zero, it is set to 1.0 for C and 0.9 for R culverts.

Not used for outlet controlled flow regimes. 		Float
19 EntryC_or_WSa The entry loss coefficient for outlet controlled flow (recommended value of 0.5). If value exceeds 1.0, it is set to 1.0. If value is less than zero (0), it is set to zero (0). If Structure Losses == ADJUST (the default) or the A flag is used (see Table 5.30), this value is adjusted according to the approach flow velocity (see Section 5.7.7). If the culvert is discharging out of a manhole, this attribute is ignored and the entry loss used is that determined by the upstream manhole based on the manhole energy losses formulation (see Section 5.10.4). The entry loss value used in the computation can be viewed over time using the _TSL output layer (see Section 15.2.4) or the QGIS TUFLOW Viewer plugin. Float
20 ExitC_or_WSb The exit loss coefficient for outlet controlled flow (recommended value of 1.0). If value exceeds 1.0, it is set to 1.0. If value is less than zero (0), it is set to zero (0). If Structure Losses == ADJUST (the default) or the A flag is used (see Table 5.30), this value is adjusted according to the departure velocity (see Section 5.7.7). If the culvert is discharging into a manhole, this attribute is ignored and the exit loss used is that determined by the downstream manhole based on the manhole energy losses formulation (see Section 5.10.4). The exit loss value used in the computation can be viewed over time using the _TSL output layer (see Section 15.2.4) or the QGIS TUFLOW Viewer plugin. Float
Table 5.6: 1D Culvert Flow Regime Flags
Regime Description
A Unsubmerged entrance and exit. Critical flow at entrance. Upstream controlled with the flow control at the inlet.
B Submerged entrance and unsubmerged exit. Orifice flow at entrance. Upstream controlled with the flow control at the inlet. For circular culverts, not available for Culvert Flow == Method A.
C Unsubmerged entrance and exit. Critical flow at exit. Upstream controlled with the flow control at the culvert outlet.
D Unsubmerged entrance and exit. Sub-critical flow at exit. Downstream controlled.
E Submerged entrance and unsubmerged exit. Full pipe flow. Upstream controlled with the flow control at the culvert outlet.
F Submerged entrance and exit. Full pipe flow. Downstream controlled.
G No flow. Dry or flap-gate active.
H Submerged entrance and unsubmerged exit. Adverse slope. Downstream controlled.
J Unsubmerged entrance and exit. Adverse slope. Downstream controlled.
K Unsubmerged entrance and submerged exit. Critical flow at entrance. Upstream controlled with flow control at the inlet. Hydraulic jump along culvert. Not available for Culvert Flow == Method A.
L Submerged entrance and exit. Orifice flow at entrance. Upstream controlled with the flow control at the inlet. Hydraulic jump along culvert. Not available for Culvert Flow == Method A.
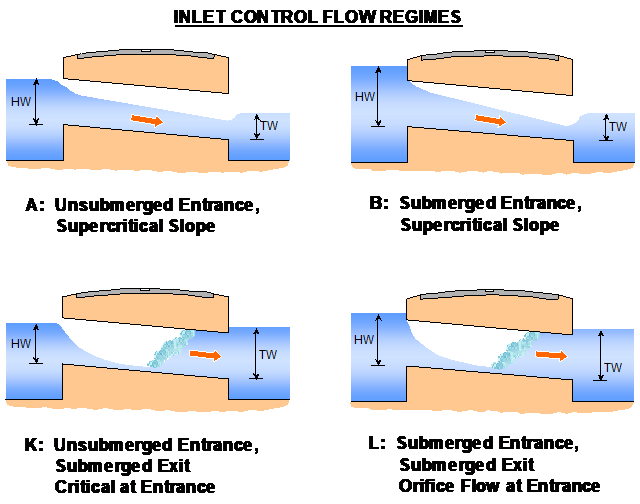
**1D Inlet Control Culvert Flow Regimes**

Figure 5.4: 1D Inlet Control Culvert Flow Regimes

**1D Outlet Control Culvert Flow Regimes**

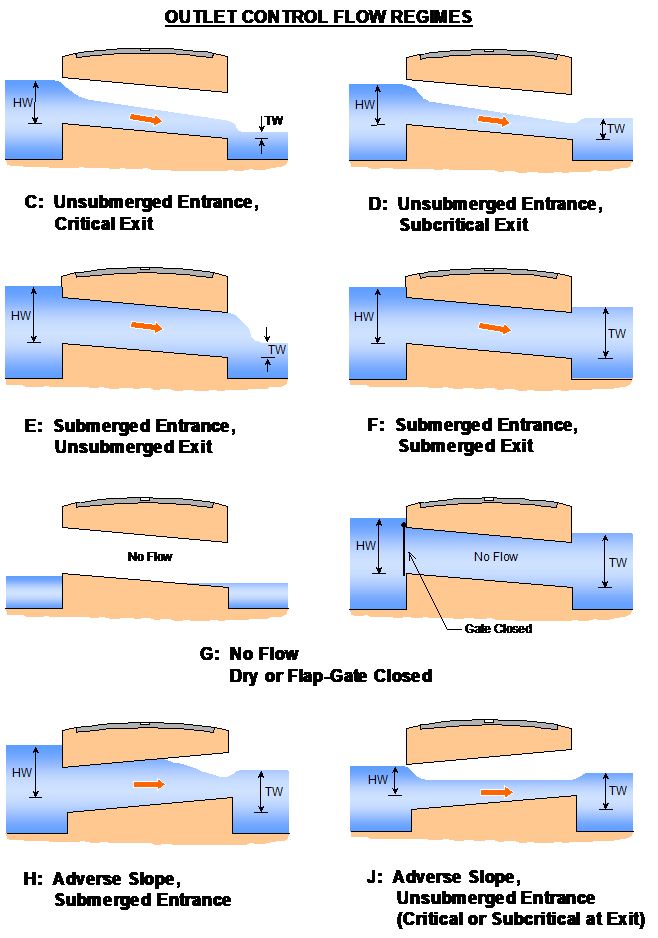
Figure 5.5: 1D Outlet Control Culvert Flow Regimes

5.7.1.1 Blockage Matrix

This feature allows for blockage of culverts to be varied based on the Average Recurrence Interval (ARI) of the flood simulation. This applies to C (circular) and R (rectangular) type culverts. For Australian users, this hydraulic structure blockage option is consistent with Project 11 of Australian Rainfall & Runoff (Weeks et al., 2013).

Two different blockage methods are available:

  1. The first method reduces the area in the culvert;
  2. The second applies a modified energy loss value to account for the blockage.

Please refer to Ollett & Syme (2016) for background information on the loss approaches.

Each culvert can be assigned a blockage category, which is defined in the 1d_nwk pBlockage attribute as a character field. A matrix of blockage category and percentage blockage for a range of ARIs is defined. Please see Section 5.7.1.1.4 for guidance on implementation.

5.7.1.1.1 Reduced Area Method

For the reduced area method, the culvert area is reduced to match the specified blockage in the same manner as varying the pBlockage attribute on the 1d_nwk layer (refer to Table 5.5). For example, with a blockage value of 10 the culvert area is reduced by 10%.

5.7.1.1.2 Energy Loss Method

For this method the area of the culvert is not modified, however, an increased entrance energy loss is applied. The modified energy loss is based on the specified culvert entry loss and the blockage ratio as per equation (5.4) (Witheridge, 2009):

\[\begin{equation} C_{ELC\_ modified} = \left( \frac{1 + \sqrt{C_{ELC}}}{BR} - 1 \right)^{2} \tag{5.4} \end{equation}\]

Where:

  • \(C_{ELC\_ modified}\) = Modified culvert entry loss value
  • \(C_{ELC}\) = Specified culvert entry loss value
  • \(BR\) = Blockage ratio (area of blocked culvert / area unblocked culvert)

When BR is 1 (unblocked), the modified entry loss coefficient becomes the specified entry loss coefficient. The modified coefficients for a range of blockages are provided in Table 5.7.

Table 5.7: Computed Values of Modified Energy Loss Coefficient
CELC
0.3 0.5 0.7
Specified % Blockage BR CELC_modified
0 1 0.3 0.5 0.7
10 0.9 0.5 0.8 1.1 
25 0.75 1.1  1.6 2.1
50 0.5 4.4  5.8 7.1
75 0.25 27 34 40
90 0.1 210 260 300
95 0.05 900 1100 1280
100 0 ∞ ∞ ∞

Whilst loss values of greater than 1.0 may appear counter-intuitive, it is appropriate in this situation. In conduit hydraulics there are two types of loss coefficients that are used to represent constrictions, one type being applied to the velocity at the constriction itself (these are always <=1), and the other type which are applied to the full-barrel velocity downstream of the blockage where the loss coefficient may approach infinity. The second type is convenient as the velocity downstream of the blockage is readily available and requires no manipulation of culvert geometry, and follows in principle the same application of valve coefficients. The equation above simply gives the conversion between these two types of loss coefficients.

Note: The minimum blockage ratio is set to 0.001 or 0.1%. This is required to avoid a divide by zero error in the calculations. This loss method only applies when the culvert is operating under outlet control. For an inlet control flow regime no energy loss is applied, the reduced area method is used instead.

5.7.1.1.3 Blockage Matrix Commands

The commands available for the Blockage Matrix method are listed in Table 5.8.

Table 5.8: Commands for the Blockage Matrix Method
Command Description
Blockage Matrix Turns on or off the blockage matrix functionality outlined in this section. The default is for this feature to be off.
Blockage Matrix File Specifies a blockage file containing the blockage values for the various blockage categories and ARI values.
Blockage Method Specifies whether to use RAM (Reduced Area Method) or ELM (Energy Loss Method). No default approach is applied. This command must be specified if using the blockage matrix functionality.
Blockage ARI Specifies the ARI for the current simulation. This would typically be defined in an event file (.tef).
Blockage Override Sets the blockage for all culverts with the specified blockage category. This option is useful for running simulations under an “all clear” case.
Blockage Default Sets the blockage category for culverts that do not have a blockage type specified (including those that have a numeric pBlockage defined)
Blockage PMF ARI If PMF has been specified in the ARI column of the blockage matrix, this command sets an ARI to be used for the PMF. This allows for interpolation of blockages for ARI values up to the PMF.
5.7.1.1.4 Implementation

To make use of this feature the 1d_nwkb GIS layer may be used. This layer is identical to the 1d_nwk layer but the pBlockage attribute of the layer is a character field instead of a float (numeric) type. See Table 5.9. This has not been made the default field type in the 1d_nwk empty (template) files that TUFLOW produces, for two main reasons:

  • A character field is bigger and less efficient to read, this could slow down simulation start-up for models not using the blockage categories; and
  • A numeric field (in almost all GIS packages) defaults to 0.0, i.e. no blockage. This is not the case for a character field.

As an alternative to the 1d_nwkb GIS layer, the pBlockage attribute of the 1d_nwk GIS layer can be changed from a float (numeric) type to a character field, with maximum width of 50. Instructions on how to change the GIS layer attribute type in QGIS, ArcMap and MapInfo are provided in the TUFLOW Wiki as per the links below:

Table 5.9: Blockage: 1D Model Network (1d_nwkb) Attribute Descriptions
No.  Default GIS Attribute Name Description Type
1 ID Same as for Table 5.5. Char(12)
2 Type Same as for Table 5.5. Char(4)
3 Ignore Same as for Table 5.5. Char(1)
4 UCS
(Use Channel Storage at nodes) 		Same as for Table 5.5. Char(1)
5 Len_or_ANA Same as for Table 5.5. Float
6 n_nF_Cd Same as for Table 5.5. Float
7 US_Invert Same as for Table 5.5. Float
8 DS_Invert Same as for Table 5.5. Float
9 Form_Loss Same as for Table 5.5. Float
10 pBlockage

C, R Channel Type: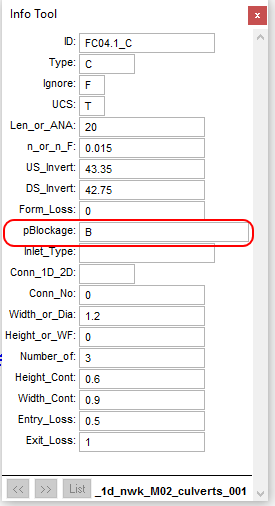
Either a numberic value (See Table 5.5) or the blockage category name as a character string (e.g. “A”). If left blank, the Blockage Default would apply. In the example below, the pBlockage attribute has been set to a category named “B”.

I Channel Type:
Not used.

To apply a blockage to irregular shaped structures, see the skew angle attribute within Table 5.4. 		Char(50)
11 Inlet_Type Not used. Char(256)
12 Conn_1D_2D Not used. Char(4)
13 Conn_No Not used. Integer
14 Width_or_Dia Same as for Table 5.5. Float
15 Height_or_WF Same as for Table 5.5. Float
16 Number_of Same as for Table 5.5. Integer
17 HConF_or_WC Same as for Table 5.5. Float
18 WConF_or_WEx Same as for Table 5.5. Float
19 EntryC_or_WSa Same as for Table 5.5. Float
20 ExitC_or_WSb Same as for Table 5.5. Float

Each blockage category must be defined in the Blockage Matrix File. The first column should contain the Average Recurrence Interval (ARI) for a range of events, any additional columns contain percentage blockages for each of the ARIs. An example blockage matrix file is provided in Table 5.10 containing 5 different blockage categories (A, B, C, D, E). For blockage category A the culvert is unblocked for all ARIs, for category E the culvert is fully blocked for all ARIs. For the categories B, C, and D the blockage varies by ARI.

If the specified ARI sits between the defined ARI values in the blockage matrix file a linear interpolation is used. For example, in the table below for a 50-year ARI, blockage category “C” will have a blockage of 13.75%.

Table 5.10: Example Blockage Matrix File
ARI A B C D E
1 0 10 10 10 100
20 0 10 10 20 100
100 0 10 20 50 100
2000 0 20 50 70 100
10000 0 50 70 100 100

The ARI values for the blockage matrix file should be in ascending order. “PMF” can be defined in the ARI column, if this is done, an ARI must be assigned to the PMF using the command Blockage PMF ARI.

Example TUFLOW commands

.tcf file commands

Blockage Matrix == On
Blockage Matrix File == Matrix_Blockages.csv
Blockage Method == RAM
Blockage Default == C

.tef file commands

Define Event == Q010
 Blockage ARI == 10
 BC Event Source == __ARI__ | Q010
End Define
Define Event == Q100
 Blockage ARI == 100
 BC Event Source == __ARI__ | Q100
End Define
Define Event == QPMF
 Blockage ARI == 100000
 BC Event Source == __ARI__ | PMF
End Define

A working example of a blockage matrix model is provided in the 1D Structures Example Model Dataset on the TUFLOW Wiki.

5.7.1.2 Limitations

For the energy loss method, the loss value only applies to the culverts when flowing in outlet control flow regimes. When the flow conditions are inlet controlled TUFLOW reverts to using the reduced area method. This is required, as there is no guidance how to adjust the contraction coefficients or otherwise as used by the inlet controlled culvert equations.

5.7.2 Bridges

5.7.2.1 Bridges Overview

Bridge channels do not require data for length, Manning’s n, divergence or bed slope (they are effectively zero-length channels, although the length is used for automatically determining nodal storages – see Section 5.12.1.1). The bridge opening cross-section is described in the same manner to a normal channel.

Two types of bridge channels can be specified:

  • “B” bridges require the user to specify an energy loss versus elevation table, usually derived from loss coefficients in the literature such as “Hydraulics of Bridge Waterways” (Bradley, 1978) or “Guide to Bridge Technology Part 8, Hydraulic Design of Waterway Structures” (Austroads, 2018). The energy loss table can be generated automatically via the 1d_nwk Form_Loss attribute if the energy loss coefficient is constant up to the underside of the bridge deck.
  • “BB” bridges automatically calculate the form (energy) losses associated with the approach and departure flows as the water constricts and expands. It also automatically applies bridge deck losses associated with pressure flow. The only user specified loss coefficients required for BB bridges are the pier losses and the deck losses once fully submerged. If the pier loss coefficient is constant through the vertical the coefficient can simply be specified via the 1d_nwk Form_Loss attribute as described further below.

For B bridges, two bridge flow approaches are offered using Bridge Flow. Method B is an enhancement on Method A by providing better stability at shallow depths or when wetting and drying. There are also some subtle differences between the methods in how the loss coefficients are applied at the bridge deck. This is discussed further below. Method B is the approach recommended with Method A provided for legacy models. For Bridge Flow == Method A, the underside of the bridge deck (the obvert or soffit) is taken as the elevation when the flow area stops increasing, or the highest elevation in the bridge’s cross-section data, whichever occurs first. For Bridge Flow == Method B, the highest (last) elevation in the cross-section table is always assumed to be the underside of the bridge deck.

5.7.2.2 Bridge Cross-Section and Loss Tables

The cross-sectional shape of the bridge is specified in the same manner as for open channels using a 1d_xs GIS layer (refer to Section 5.6 and Table 5.4) and the command Read GIS Table Links. The line is digitised midway across the 1d_nwk channel line (do not specify as an end cross-section, i.e. a cross-section line snapped to an end of the bridge channel). As per the open channel, the cross-section data can be in offset-elevation (XZ) or height-width (HW) format.

Bridge structures are modelled using a height varying form or energy loss coefficient. A table (referred to as a Bridge Geometry “BG” or Loss Coefficient “LC” Table) of backwater or form loss coefficient versus height is required. The interpretation of loss coefficients provided by the user differs depending on whether the bridge channel is of a B or BB type as discussed in the following sections.

BG Tables can be entered using .csv files via a 1d_bg GIS layer (see Table 5.12) using the command Read GIS Table Links. A line is digitised crossing the 1d_nwk channel in the same manner as for the 1d_xs GIS layer used to define the cross-sectional shape of the bridge. The line does not have to be identical to the cross-section line.

Where the loss coefficient is constant through to the bridge deck (e.g. no losses such as a clear spanning bridge, or pier losses only – see BB bridges), the BG table can automatically be created by specifying a positive non-zero value for the Form_Loss attribute in the 1d_nwk layer (see Table 5.11). How the Form_Loss attribute is interpreted differs between B and BB bridge channels as discussed in the following sections.

Any wetted perimeter or Manning’s n inputs in the hydraulic properties table are ignored. If the flow is expected to overtop the bridge, a parallel weir channel should be included to represent the flow over the bridge deck, or a BW or BBW channel can be specified (see Section 5.7.4.5).

5.7.2.3 B Bridge Losses Approach

The coefficients for B bridges are usually obtained from publications such as “Hydraulics of Bridge Waterways” (Bradley, 1978) or “Guide to Bridge Technology Part 8, Hydraulic Design of Waterway Structures” (Austroads, 2018), through the following procedure.

  • The bridge opening ratio (stream constriction ratio), defined in Equations 1 and 2 of “Hydraulics of Bridge Waterways” (Bradley, 1978), is estimated for various water levels from the local geometry. Alternatively, the bridge opening ratio is estimated with the help of a trial modelling run in which the stream crossed by the bridge is represented by a number of parallel channels, providing a more quantitative basis for estimating the proportion of flow obstructed by the bridge abutments.
  • For each level this enables the value of Kb to be obtained from Figure 6 of “Hydraulics of Bridge Waterways” (Bradley, 1978). Additional factors, for piers (Kp from Figure 7), eccentricity (Ke from Figure 8) and for skew (Ks from Figure 10) make up the primary contributors to Kb.
  • The backwater coefficient Kb input into the LC table is the sum of the relevant coefficients at each elevation. The velocity through the bridge structure used for determining the head loss is based on the flow area calculated using the water level at the downstream node.

Backwater coefficients derived in this manner have usually taken into account the effects of approach and departure velocities (via consideration of the upstream and downstream cross-section areas), in which case the losses for the B channel should be fixed. This is the default setting or can be manually specified using the “F” flag (i.e. a “BF” channel) in the 1d_nwk Type attribute, or use Structure Losses == ADJUST EXCEPT BG TABLES (the default).

For Bridge Flow == Method A, once the downstream water level is within 10% of the flow depth under the bridge, a bridge deck submergence factor is phased in by applying a correction for submerged decking using a minimum value of 1.5625 (if the specified loss coefficient is greater than 1.5625, this value is applied). Bridge Flow == Method B does not use the 10% of the flow depth phasing in nor applies a minimum loss coefficient once the bridge deck is submerged (i.e. it applies the value as per the specified loss coefficients (BG) table). Method B relies on the user to provide appropriate values at all flow heights.

The value of 1.5625 is derived from the following equation (5.5) presented in Waterway Design - A Guide to the Hydraulic Design of Bridges, Culverts and Floodways (Austroads, 1994):

\[\begin{equation} Q = {C_d}{b_N}Z\sqrt{2gdH} \tag{5.5} \end{equation}\]

Where:

  • Q = Total discharge (m3/s or ft3/s)
  • Cd = Coefficient of discharge (0.8 for a surcharged bridge deck)
  • bN = Net width of waterway (m or ft)
  • Z = Vertical distance under bridge to mean river bed (m or ft)
  • dH = Upstream energy (or water surface) level minus downstream water surface level (m or ft)

Note: Metric (SI) units are TUFLOW’s default. To use imperial units, ensure Units == US Customary has been specified in the .tcf.

Assuming \({V} = \frac{Q}{b_{N}Z}\) and \(dh = K\frac{V^2}{2g}\), the equation rearranges to give \(K = \frac{1}{C_d^2}\), where a Cd value of 0.8 equates to a K energy loss value of 1.5625.

5.7.2.4 BB Bridge Losses Approach

BB bridges break down the energy losses into the following categories:

  • Bridge pier losses;
  • Losses due to flow contraction and expansion;
  • Bridge deck losses when the bridge is submerged but not under pressure flow condition; and
  • If under pressure flow, the pressure flow equation is applied as described further below.

BB bridges differ from B bridges in that the losses due to flow contraction and expansion, and the occurrence of pressure flow are handled automatically. The only loss coefficient required to be specified is that due to piers (via the Form_Loss attribute value or a LC table). Other loss parameters can be either set based on the default parameters, or can be specified by users. The parameters used by the BB bridge routine are:

  • Cd = the Bridge Deck surcharge coefficient (Default = 0.8).
  • DLC = the Deck loss coefficient (Default = 0.5) and only applies when no LC table exists and an automatically generated table using the 1d_nwk Form_Loss attribute is created.
  • ELC = the unadjusted entry loss coefficient (Default = 0.5).
  • XLC = the unadjusted exit loss coefficient (Default = 1.0).

The .ecf command “Bridge Zero Coefficients == <CD>, <DLC>, <ELC>, <XLC>” can be used to change the above default values to the user’s own default values.

The above values can also be changed for an individual bridge using the following 1d_nwk attributes. If the attribute value is zero then the default value or the value specified by Bridge Zero Coefficients is used.

  • CD = HConF_or_WC
  • DLC = WConF_or_WEx
  • ELC = EntryC_or_WSa
  • XLC = ExitC_or_WSb

The entrance and exit losses are adjusted every timestep according to the approach and departure velocities based on the equations below from Section 5.7.7. This approach yields similar results to the approach for determining contraction and expansion losses in publications such as “Hydraulics of Bridge Waterways” (Bradley, 1978) or “Guide to Bridge Technology Part 8, Hydraulic Design of Waterway Structures” (Austroads, 2018).

\[\begin{equation} C_{ELC\text{_}adjusted} = C_{ELC}\left\lbrack 1 - \frac{V_{approach}}{V_{structure}} \right\rbrack \tag{5.6} \end{equation}\]

\[\begin{equation} C_{XLC\text{_}adjusted} = C_{XLC}\left\lbrack 1 - \frac{V_{departure}}{V_{structure}} \right\rbrack^{2} \tag{5.7} \end{equation}\]

Where:

  • V = Velocity (m/s or ft/s if using Units == US Customary)
  • C = Energy Loss Coefficient

Pressure flow is handled by transitioning from the equation described in the previous section (to derive the K value of 1.5625 from a coefficient of discharge value of 0.8) to a fully submerged situation where a deck energy loss is applied. The flux is calculated based on both the fully submerged situation and the pressure flow situation, and the lesser of the two fluxes is applied. The 1d_nwk HConF_or_WC attribute can be used to vary Cd (default value is 0.8) and the WConF_or_WEx attribute to set the submerged deck loss coefficient. When pressure flow results the “P” flag will appear in the .eof file and _TSF layer.

Optionally, LC tables can be specified for BB bridges. If a LC table exists, the Deck loss coefficient (DLC) will be ignored, while the other 3 parameters (CD, ELC and XLC) are not affected. The LC tables for BB bridges should only be the losses due to piers and bridge decks. The LC table should not include any losses for contraction, expansion and pressure flow. Note the Form_Loss value is added to the LC table loss values.

If no LC table exists for the BB bridge, and the 1d_nwk Form_Loss attribute is greater than 0.0001, a LC table is automatically generated using Form_Loss for the pier losses and the WConF_or_WEx for the Deck Loss coefficient (DLC).

Other notes are:

  • BB bridges are only available if Structure Routines == 2013 (the default).
  • The unadjusted entry and exist losses (ELS and XLC) cannot be below 0 or greater than 1, and will be automatically limited to these values.
  • _TSF and _TSL layers contain the following flags/values for BB bridges:
    • For normal flow (“ ” or “D” if drowned out): fixed / adjusted components
    • For Pressure (“P”) flow: Deck surcharge Coefficient / 0.0
    • Other flags:
      • “U” for upstream controlled flow – only occurs when downstream water level is below the bridge bed level.
      • “Z” for zero or nearly zero flow.

A working example of a model containing an BB bridge is provided in the 1D Structures Example Model Dataset on the TUFLOW Wiki.

Table 5.11: Bridges: 1D Model Network (1d_nwk) Attribute Descriptions
No.  Default GIS Attribute Name Description Type
1 ID Unique identifier up to 12 characters in length. It may contain any character except for quotes and commas, and cannot be blank. As a general rule, spaces and special characters (e.g. “\”) should be avoided, although they are accepted. The same ID can be used for a channel and a node, but no two nodes and no two channels can have the same ID. Char(12)
2 Type “B” or “BB” as specified in Table 5.1. Char(4)
3 Ignore If a “T”, “t”, “Y” or “y” is specified, the object will be ignored (T for True and Y for Yes). Any other entry, including a blank field, will treat the object as active. Char(1)
4 UCS
(Use Channel Storage at nodes). 		If left blank or set to Yes (“Y” or “y”) or True (“T” or “t”), the storage based on the width of the channel over half the channel length is assigned to both of the two nodes connected to the channel. If set to No (“N” or “n”) or False (“F” or “f”), the channel width does not contribute to the node’s storage. See Section 5.12 for further discussion. Char(1)
5 Len_or_ANA Only used in determining nodal storages if the UCS attribute is set to “Y” or “T”. Not used in conveyance calculations. Float
6 n_nF_Cd Not used. Float
7 US_Invert Sets the upstream and downstream inverts. Note that the invert is taken as the maximum of the US_Invert and the DS_Invert attributes. Use -99999 to use the bed of the cross-section as the invert. Float
8 DS_Invert Sets the downstream invert of the channel using the same rules as for described for the US_Invert attribute above. Float
9 Form_Loss

If a LC table exists, for BB bridges adds the value specified to the loss coefficients in the LC table. Not added to LC tables for B bridges.

If no LC table exists, and the value is greater than zero, TUFLOW automatically generates a LC table of constant loss coefficient up until the bridge deck (i.e. the top of the cross-section). The interpretation of the LC table generated from the Form_Loss value differs depending on whether a B or a BB bridge as follows:

For B bridges (with no LC table):

  • The Form_Loss (LC value) is not subject to adjustment when using Structure Losses == ADJUST.
  • Above the underside of the bridge deck (the top of the cross-section) a value of 1.5625 is used, with the 1.5625 less the Form_Loss value is subject to adjustment when using Structure Losses == ADJUST.

For BB bridges (with no LC table):

  • The Form_Loss (LC value) is only used to apply pier losses. Contraction/expansion losses and bridge deck pressure flow losses are automatically calculated.
  • Once the bridge deck is fully submerged (and no longer under pressure flow) the WConF_or_WEx attribute is used to set the additional losses due to the bridge deck.
Note: Due to the potential for a divide by zero, a zero loss value cannot be specified with no LC table. A loss value of 0 will return ERROR 1422. A minimum loss value of 0.01 for B bridges or 0.001 for BB bridges is required by TUFLOW to ensure a divide by zero does not occur. Specifying a loss value equal to or less than these minimums (but not 0) will apply these minimum losses, i.e. to apply these minimum losses specify a value of 0.001 for either B or BB bridges. 		Float
10 pBlockage Not used. Reserved for future builds to fully or partially block B channels. The 1d_xs Skew attribute can be used to partially block cross-sections of these channels – see Table 5.4. Float
11 Inlet_Type Leave blank unless using the legacy MIKE 11 1D cross-section data feature. Char(256)
12 Conn_1D_2D Leave blank unless using the legacy MIKE 11 1D cross-section data feature, or if accessing a Flood Modeller cross-section database (.pro file), enter the label in the .pro file. Char(4)
13 Conn_No Leave blank unless using the legacy MIKE 11 1D cross-section data feature. Integer
14 Width_or_Dia Not used. Float
15 Height_or_WF Not used. Float
16 Number_of Not used. Integer
17 HConF_or_WC

B bridges: Not used.

BB bridges: Bridge deck pressure flow contraction coefficient (Cd). If set to zero the default of 0.8 or that specified by Bridge Zero Coefficients is used. 		Float
18 WConF_or_WEx

B bridges: Not used.

BB bridges: Bridge deck energy loss coefficient (DLC) for fully submerged flow. If set to zero the default of 0.5 or that specified by Bridge Zero Coefficients is used. 		Float
19 EntryC_or_WSa

B bridges: Not used.

BB bridges: Unadjusted entrance energy loss coefficient (ELC). If set to zero the default of 0.5 or that specified by Bridge Zero Coefficients is used. 		Float
20 ExitC_or_WSb

B bridges: Not used.

BB bridges: Unadjusted exit energy loss coefficient (XLC). If set to zero the default of 1.0 or that specified by Bridge Zero Coefficients is used. 		Float
Table 5.12: 1D Bridge Geometry Table Link (1d_bg) Attribute Descriptions
No.  Default GIS Attribute Name Description Type
1 Source Filename (and path or relative path if needed) of the file containing the tabular data. Must be a comma or space delimited text file such as a .csv file. Char(50)
2 Type “BG” or “LC”: Bridge energy loss coefficients (second column) versus elevation (first column) for bridge structures. Char(2)
3 Flags No optional flags. Char(8)
4 Column_1

Optional. Identifies a label in the Source file that is the header for the first column of data (ie. elevation). Values are read from the first number encountered below the label until a non-number value, blank line or end of the file is encountered.

If this field is left blank, the first column of data in the Source file is used. 		Char(20)
5 Column_2

Optional. Identifies a label in the Source file that is in the header for the second column of data (ie. loss coefficient).

If this field is left blank, the next column of data after Column_1 is used. 		Char(20)
6 Column_3 Not used. Char(20)
7 Column_4 Not used. Char(20)
8 Column_5 Not used. Char(20)
9 Column_6 Not used. Char(20)
10 Z_Increment Not used. Float
11 Z_Maximum Not used. Float
12 Skew
(in degrees) 		Not used. Float

5.7.3 Arch Bridge

The 2023-03 release introduced support for arch bridges as 1D channels. The approach is based on the ‘Afflux at Arch Bridges’ (HR Wallingford, 1988). Arch bridges are defined in the 1d_nwk layer as a “BArch” type. The 1d_nwk attributes specific to an arch bridge are outlined below in Table 5.13.

When an arch bridge becomes fully submerged, the actual flux through a small arch bridge opening can diverge from the flux calculated from the approach above. By default, the arch bridge approach (HR Wallingford, 1988) is still applied when water level exceeds the bridge obvert (or soffit) level. However, a transition to orifice flow condition can be optionally turned on.
The flow rate under the orifice flow condition is calculated using Equation (5.22) with the discharge coefficient (\(C_{d}\)) set via the HConF_or_WC attribute (detailed in Table 5.13). Two options are available to calculate the final discharge coefficient based on the input 1d_nwk HConF_or_WC attribute:

  1. A positive HConF_or_WC value can be used to set the discharge coefficient. The recommended value is 0.799.
  2. If a negative value is specified, the absolute of HConF_or_WC is used as a calibration factor, i.e. the discharge coefficient = abs(HConF_or_WC) * 0.799. For example, a HConF_or_WC value of -2 will adjust the discharge coefficient to 1.598.

To enable this transition, three extra attributes must be specified: a discharge coefficient (or calibration factor), lower transition distance and upper transition distance (HConF_or_WC, EntryC_or_WSa and ExitC_or_WSb attributes outlined in Table 5.13). The transition from bridge flow to orifice flow will begin at the lower transition elevation and continue linearly until the upper transition elevation is reached. From this point, the orifice flow condition is used.

A working example of a model containing an arch bridge is provided in the 1D Structures Example Model Dataset on the TUFLOW Wiki.

Table 5.13: Arch Bridges 1D Model Network (1d_nwk) Attribute Descriptions
No.  Default GIS Attribute Name Description Type
1 ID Unique identifier up to 12 characters in length. It may contain any character except for quotes and commas, and cannot be blank. As a general rule, spaces and special characters (e.g. “\”) should be avoided, although they are accepted. The same ID can be used for a channel and a node, but no two nodes and no two channels can have the same ID. Char(12)
2 Type “BArch” as specified in Table 5.1. Char(4)
3 Ignore If a “T”, “t”, “Y” or “y” is specified, the object will be ignored (T for True and Y for Yes). Any other entry, including a blank field, will treat the object as active. Char(1)
4 UCS
(Use Channel Storage at nodes). 		If left blank or set to Yes (“Y” or “y”) or True (“T” or “t”), the storage based on the width of the channel over half the channel length is assigned to both of the two nodes connected to the channel. If set to No (“N” or “n”) or False (“F” or “f”), the channel width does not contribute to the node’s storage. See Section 5.12 for further discussion. Char(1)
5 Len_or_ANA Only used in determining nodal storages if the UCS attribute is set to “Y” or “T”. Not used in conveyance calculations. Float
6 n_nF_Cd Not used. Float
7 US_Invert Sets the upstream and downstream inverts. Note that the invert is taken as the maximum of the US_Invert and the DS_Invert attributes. Use -99999 to use the bed of the cross-section as the invert. Float
8 DS_Invert Sets the downstream invert of the channel using the same rules as for described for the US_Invert attribute above. Float
9 Form_Loss Not used. Float
10 pBlockage Not used. Float
11 Inlet_Type The relative path to the arch properties file (must be a .csv file). See Section 5.8.1. Char(256)
12 Conn_1D_2D Not used. Char(4)
13 Conn_No Not used. Integer
14 Width_or_Dia Optional skew parameter. Float
15 Height_or_WF Optional calibration coefficient. Float
16 Number_of Not used. Integer
17 HConF_or_WC

Discharge coefficient (\(C_{d}\)) for orifice flow (see Equation (5.22)). To enable the transition to orifice flow, specify a non-zero value for this attribute.

  • A positive value sets the discharge coefficient. The recommended value is 0.799.
  • If a negative value is specified, the absolute of this value is used as a calibration factor. I.e. discharge coefficient = abs(calibration factor) * 0.799.
  • If left blank, or set to 0, the orifice flow is not applied.
If this field is specified, attributes EntryC_or_WSa and ExitC_or_WSb must also be set. 		Float
18 WConF_or_WEx Not used. Float
19 EntryC_or_WSa

Lower transition distance for orifice flow, measured as the depth below obvert. I.e. the depth below obvert at which the transition from bridge flow to orifice flow commences.

This field is ignored if HConF_or_WC is blank. 		Float
20 ExitC_or_WSb

Upper transition distance for orifice flow, measured as the depth above obvert. I.e. the depth above obvert at which the transition from bridge flow to orifice flow is complete.

The upper transition elevation must be greater than the lower transition elevation.

This field is ignored if HConF_or_WC is blank. 		Float

The .csv for the arch properties should contain the columns outlined in Table 5.14.

Table 5.14: Arch Bridge Properties .csv
Column Description
1 Start chainage for arch opening.
2 End chainage for arch opening.
3 Springing level.
4 Start chainage for arch opening.

5.7.3.1 Arch Bridge Editor

An arch bridge creator and editor tool has been developed for the QGIS TUFLOW Plugin. This tool is available from the TUFLOW Plugin Version 3.7 or later. The documentation and examples for this tool can be found on the TUFLOW Wiki Arch Bridge Editor.

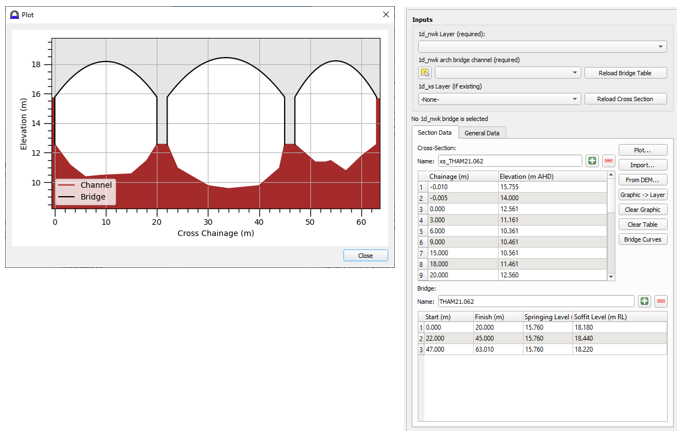
**Arch Bridge Editor Tool**

Figure 5.6: Arch Bridge Editor Tool

5.7.3.2 Arch Minimum Blockage

The flume experiments in the ‘Afflux at Arch Bridges’ (HR Wallingford, 1988) were done using medium to high bridge blockages (20%~70%), and this approach can generate extremely high velocity when the bridge blockage is close to zero percent. The 2023-03-AF release introduced a minimum blockage of 5% to stabilise the flow. This default value can be changed using the following command:

Arch Bridge Minimum Blockage (%) == <min_pblockage>

5.7.4 Weirs

5.7.4.1 Weirs Overview

A range of weir types are available as listed in Table 5.15. Weir channels do not require data for length, Manning’s n, divergence or bed slope (they are effectively zero-length channels, although the length is used for automatically determining nodal storages – see Section 5.12.1.1).

All weirs have three flow regimes of zero flow (dry), upstream controlled flow (unsubmerged) and downstream controlled flow (submerged).

Table 5.15: Weir Types
Weir Type Description
W The original ESTRY weir based on the broad-crested weir formula with the Bradley submergence approach (see Weir Approach == METHOD A). The weir shape is defined either as a rectangle using the 1d_nwk Width attribute or as a cross-section.
WB Broad-crested weir. A rectangular section shape is assumed.
WC Crump weir.
WD User-defined weir.
WO Ogee-crested weir.
WR Rectangular weir (sharp crested).
WT Trapezoidal weir or Cippoletti weir.
WV V-notch weir.
WW Similar to the original W weir channel, but has more options allowing the user to customise the weir sub-mergence curve and other parameters. Can be based on either a rectangular shape using the 1d_nwk Width attribute or on a cross-section.

5.7.4.2 Original Weirs (W)

For a “W” type weir, a standard weir flow formula is used as per the equation below. The weir is assumed to be broad-crested. Weirs with different characteristics should be modelled using one of the other weir types listed in Table 5.15 and discussed in Section 5.7.4.3.

\[\begin{equation} Q_{weir} = \ \frac{2}{3}CW\sqrt{\frac{2g}{C_{f}}}H^{\frac{3}{2}} \tag{5.8} \end{equation}\]

\[\begin{equation} V_{approach} = \ \frac{2}{3}C\sqrt{\frac{2gH}{C_{f}}} \tag{5.9} \end{equation}\]

Where:

  • \(Q_{weir}\) = Unsubmerged flow over the weir (m3/s or ft3/s)
  • \(V_{approach}\) = Velocity approaching the weir (m/s or ft/s)
  • \(C\) = Broad-crested weir coefficient of 0.57
  • \(W\) = Flow width (m or ft)
  • \(C_{f}\) = Weir calibration factor (default of 1.0 – refer to 1d_nwk “Height_or_WF” attribute)
  • \(H\) = Depth of water approaching the weir relative to the weir invert (m or ft)

Note: Metric (SI) units are TUFLOW’s default. To use imperial units, ensure Units == US Customary has been specified in the .tcf.

The calibration factor Cf, is available for modifying the flow. For a given approach velocity the backwater (head increment) of the weir channel is proportional to the inverse of the factor. It is normally set to 1.0 by default and modified if required for calibration or other adjustment. Note, this factor is not the weir coefficient, rather a calibration factor to adjust the standard broad-crested weir equation. The factor can be used to model other types of weirs through adjustment of the broad-crested weir equation, although use of the other weir types listed in Table 5.15 is recommended.

Huxley (2004) contains benchmarking of unsubmerged and submerged weir flow to the literature.

Note that the velocity output for a weir is the approach velocity, Vapproach, in the above equations, not the velocity at critical depth (when the flow is unsubmerged).

For submergence of W weir channels, it is recommended that Weir Approach is set to METHOD A or METHOD C. Both METHOD A and METHOD C utilises the Bradley submergence approach (METHOD C is a slight enhancement that only affects WW weir channels). The Bradley Submergence approach (Bradley, 1978), Figure 24, is handled by fitting the equation below to Bradley’s submergence curve reproduced in Figure 5.7 and applying the submergence factor to the weir equation above.

Once the percentage of submergence exceeds 70%, the submergence factor applied is given by the equation below (5.10). The Bradley curve (as digitised) and the resulting curve from the equation below are shown alongside the submergence curves used for other weir types. The submergence factor transitions the flow from weir flow to zero flow as the water level difference (dH) approaches zero.

\[\begin{equation} C_{sf} = \ 1 - \left( 1 - \frac{dH}{H} \right)^{20} \tag{5.10} \end{equation}\]

Weir Approach == METHOD B was introduced to provide additional stability for 1D flow over roadways connected to 2D domains, however, it can cause excessive head drops under drowned flow conditions and is not recommended or to be used with caution. METHOD B only applies to the W weir.

A working example of a model containing an original weir (W) is provided in the 1D Structures Example Model Dataset on the TUFLOW Wiki.

**Bradley Weir Submergence Curve [@Bradley1978]**

Figure 5.7: Bradley Weir Submergence Curve (Bradley, 1978)

5.7.4.3 Advanced Weirs (WB, WC, WD, WO, WR, WT, WV, WW)

The advanced weirs, as listed in Table 5.15, offer greater variety, flexibility and can be customised by the user. Most of these weirs can also be operated, see Section 5.9.

The weir flow is determined by the following equation.

\[\begin{equation} Q = {\frac{2}{3}\ {\ C}_{f\ }C}_{sf}{\ C}_{d\ }W\ \sqrt{2g}{\ H}^{Ex} \tag{5.11} \end{equation}\]

Where:

  • \(Q\) = Flow over the weir (m3/s or ft3/s)
  • \(C_{d}\) = Weir coefficient
  • \(C_{sf}\) = Weir submergence factor
  • \(C_{f}\) = Weir calibration factor (default of 1.0 – refer to 1d_nwk “Height_or_WF” attribute)
  • \(W\) = Flow width (m or ft)
  • \(H\) = Upstream water surface or energy depth relative to the weir invert (m or ft) – see note 5 below
  • \(Ex\) = Weir flow equation exponent

Note: Metric (SI) units are TUFLOW’s default. To use imperial units, ensure Units == US Customary has been specified in the .tcf.

Notes

  1. The default values for Cd are provided in Table 5.16, and documented further below for weirs where Cd is recalculated each timestep.
  2. The approach taken for calculating the weir submergence factor \(C_{sf}\) each timestep is documented below.
  3. The weir calibration factor, Cf, is by default 1.0 and should only be changed should there be a good justification.
  4. For weirs where the flow width (W) varies (e.g. a V-notch WV weir) the formula for that weir takes into account the varying width.
  5. Whether water surface depth or the energy level is used for H depends on the Structure Flow Levels setting, which can be changed on a structure by structure case using the E or H flag (see Table 5.2).
  6. The default values for Ex are provided in Table 5.16 .

Table 5.16 presents the weir coefficient \(C_{d}\) and weir flow exponent \(Ex\) used for each weir. Some of these values are derived from dimensional forms of the weir equations. Values other than the default values shown in Table 5.16 may be used by altering the attributes of the 1d_nwk layer. Refer to Table 5.17 for further information.

Note that \(C_{d}\) for WO and WV weirs is recalculated every timestep as described in the following sections. It is possible to override this by specifying a non-zero positive value for the “HConF_or_WC” attribute in the 1d_nwk layer. For WD weirs the user must specify a non-zero positive value.

The value for \(C_{f} \times C_{d}\) and \(C_{sf}\) is written to the TSL_P output (see Section 15.2.4) at each timestep.

The default submergence curves can be found in Figure 5.10 and Figure 5.10.

Table 5.16: Default Attribute Values for the Weir Equation for Different Weir Flows
Channel Type Cd (HConF or WC) Ex (WConF or WEx) a (EntryC or WSa) b (ExitC or WSb) Default Submergence Curve
SP 0.75 1.5 6.992 0.648 Ogee / Nappe (Miller, 1994; USBR, 1987)
WB 0.577  1.5 8.550 0.556 Broad-crested from Abou Seida & Quarashi, 1976 (Miller, 1994)
WC 0.508  1.5 17.870 0.590 Crump H1/Hb=1.5 (Bos, 1989)
WD User Defined 1.5 3.000 0.500 User Defined default settings
WO Recalculated every timestep 1.5 6.992 0.648 Ogee / Nappe (Miller, 1994; USBR, 1987)
WR 0.62 1.5 2.205 0.483 Sharp Crest Thin Plate from Hagar, 1987a (Miller, 1994)
WT 0.63 1.5 2.205 0.483 Sharp Crest Thin Plate from Hagar, 1987a (Miller, 1994)
WV Recalculated every timestep 2.5 2.205 0.483 Sharp Crest Thin Plate from Hagar, 1987a (Miller, 1994)
WW 0.542  1.5 21.150 0.627 Bradley 1978 Broad-crested (Bradley, 1978)
5.7.4.3.1 Ogee Crest Weir (WO)

For WO (Ogee crest) weirs, the charts developed in USBR (1987) are used by fitting the relationship presented and plotted on the USBR curve below (Figure 5.8). The relationship falls within ±0.5% of the curve. Note that the relationship below is for US Customary Units, which is converted to metric if running the simulation in metric units. The USBR (1987) method consists of two steps:

  • The ogee crest coefficient \(C_{0}\) (i.e. the discharge coefficient when the actual upstream head \(H_{e}\) = design head \(H_{0}\)) is set based on \(H_{0}\) and the height of the weir above its sill (\(P\)) as per Figure 9-23 of USBR (1987). Note that for setting the value of \(P\) the absolute difference in height between the US_Invert and DS_Invert attributes is used.
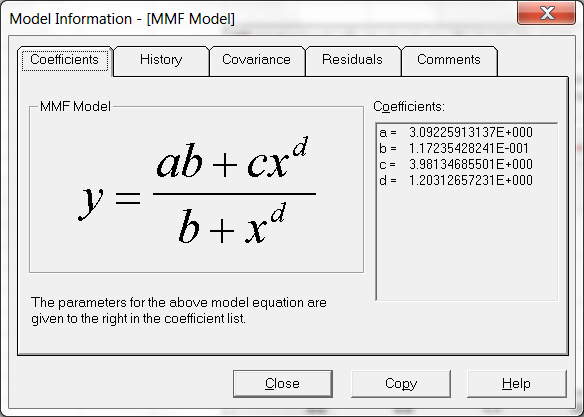
**Ogee Spillway Discharge Coefficient, based on Figure 9-23 [@USBR1987]**

Figure 5.8: Ogee Spillway Discharge Coefficient, based on Figure 9-23 (USBR, 1987)

  • When the actual head (\(H_{e}\)) is different from the design head (\(H_{0}\)) during the simulation, the discharge coefficient differs from that shown on Figure 5.8. At each simulation timestep, the discharge coefficient is adjusted based on \(H_{e}\)/\(H_{0}\) as per the chart below. The final discharge coefficient applied is \(C_{0}\) × \(C\)/\(C_{0}\) in this chart.
**Adjustment of Discharge Coefficient based on $H_{e}$/$H_{0}$, Figure 9-24 [@USBR1987]**

Figure 5.9: Adjustment of Discharge Coefficient based on \(H_{e}\)/\(H_{0}\), Figure 9-24 (USBR, 1987)

Three options to calculate the final discharge coefficient are offered based on the input value of the 1d_nwk HConF_or_WC attribute:

  • If the discharge coefficient has already been obtained by hand calculation, a positive HConF_or_WC value can be used to apply a constant discharge coefficient, i.e. \(C\) = \(C_{0}\) = HConF_or_WC.
  • If the design head (\(H_0\)) is known for an ogee crest weir, a negative HConF_or_WC value can be used to specify \(H_0\). The two-step USBR (1987) method stated above will be applied to estimate the final discharge coefficient. Note this option is only available in the 2023-03-AB build or later.
  • If HConF_or_WC is zero (0) or left as blank (the default), the actual head \(H_e\) at each simulation timestep will be used to estimate \(C\) from Figure 9-23 of USBR (1987), with no further adjustment based on Figure 9-24 of USBR (1987). This approach should be used when the design head (\(H_0\)) is unknown.
5.7.4.3.2 V-Notch Weir (WV)

For WV (V-notch) weirs, the approach taken is to use the formulae derived by LMNO Engineering as shown below. For metric models the flow is calculated in ft3/s and converted to m3/s. The top height of a V-notch weir cannot be specified, the angle continues with the increasing water level.

5.7.4.4 Advanced Weir Submergence Curves

Weir submergence factors \(C_{sf}\) were sought from two sources: “Discharge Characteristics” (Miller, 1994) and “Discharge Measurement Structures” (Bos, 1989). The submergence charts for each weir type, relating the weir submergence factor to the ratio between downstream and upstream water level were reproduced from the literature in Excel and are shown in Figure 5.11.

Two methods were utilised to fit equations to these curves. These are:

The Rational Function expressed as:

\[\begin{equation} C_{sf} = \frac{a + b\left( \frac{H_{d}}{H_{u}} \right)}{1 + c\left( \frac{H_{d}}{H_{u}} \right)\ + \ d\left( \frac{H_{d}}{H_{u}} \right)^{2}} \tag{5.12} \end{equation}\]

The Villemonte equation, expressed as:

\[\begin{equation} C_{sf} = \left( 1 - \ \left( \frac{H_{d}}{H_{u}} \right)^{a} \right)^{b} \tag{5.13} \end{equation}\]

Where:

  • \(H_{u}\) = Upstream energy or water level above the weir crest (m or ft)
  • \(H_{d}\) = Downstream energy or water level above the weir crest (m or ft)
  • \(a, b\) = Model coefficients

Note: Metric (SI) units are TUFLOW’s default. To use imperial units, ensure Units == US Customary has been specified in the .tcf.

“Discharge Measurement Structures” (Bos, 1989) applies upstream energy and downstream water level to calculate \(C_{sf}\). This can be specified globally using the Structure Flow Levels == ENERGY UPSTREAM command (the default option is “ENERGY”, which uses energy level both upstream and downstream). It can also be changed for individual weirs using the “EH” flag in the 1d_nwk “Type” attribute, e.g. “WB EH”.

For each submergence curve, the above equations were solved to obtain values for each of the variables that produced the best fit with the curves provided in the literature. After a comparison of the results, the equation from Villemonte was chosen for several reasons:

  • The Rational Function was found to be sensitive to variables and required a greater number of decimal places. Villemonte was found to provide accurate results with variables requiring only 2 decimal places.
  • The Villemonte equation contains only two variables, compared to four used in the Rational Function, making it simpler and less susceptible to error.
  • The Villemonte equation may be solved exactly at the extremities of the curves (i.e. where \(\frac{H_{d}}{H_{u}} = \ 1\) and \(C_{sf} = 0\), and when \(\frac{H_{d}}{H_{u}}\) = 0 and \(C_{sf} = 1\)). The Rational Function required further manipulation through inclusion of additional points to achieve this outcome.

The default variables a and b used to determine the submergence factor \(C_{sf}\) for each weir type are presented in Table 5.16. Figure 5.11 shows the submergence curves produced using the default values in Table 5.16 to calculate \({\ C}_{sf}\).

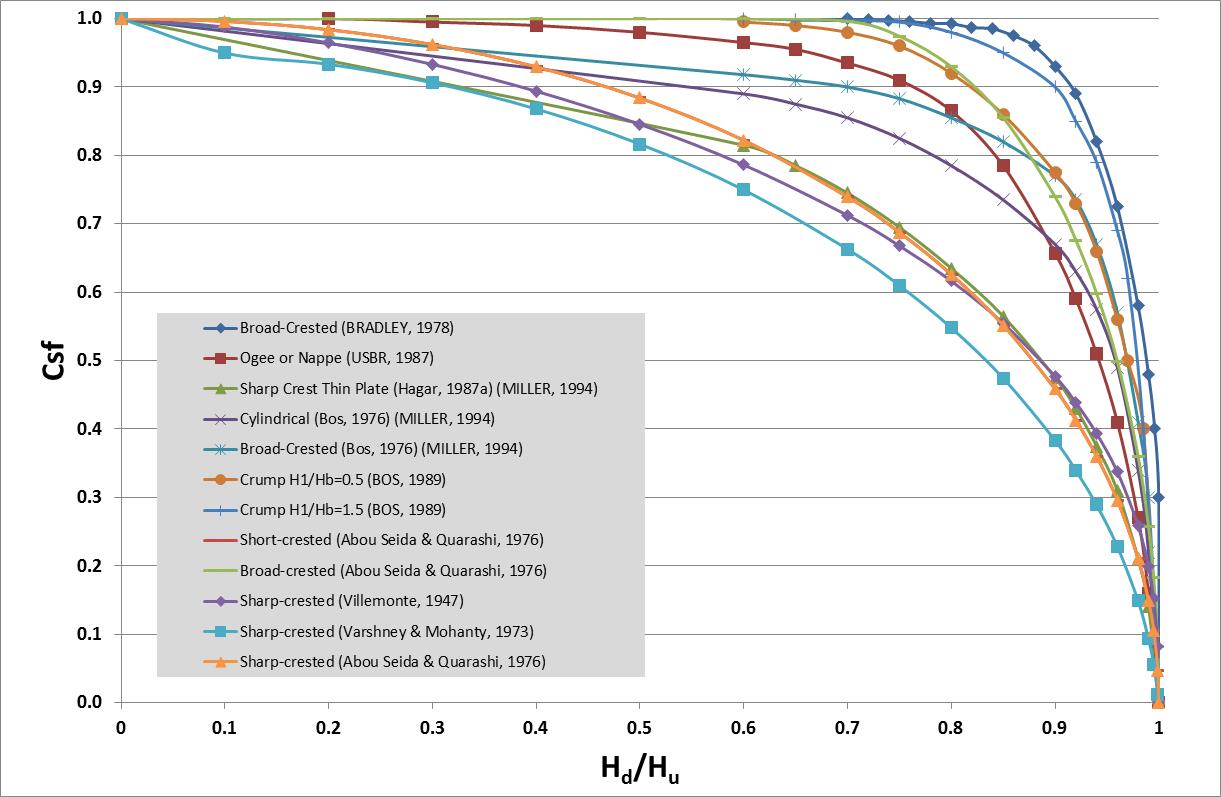
**Weir Submergence Curves from the Literature**

Figure 5.10: Weir Submergence Curves from the Literature

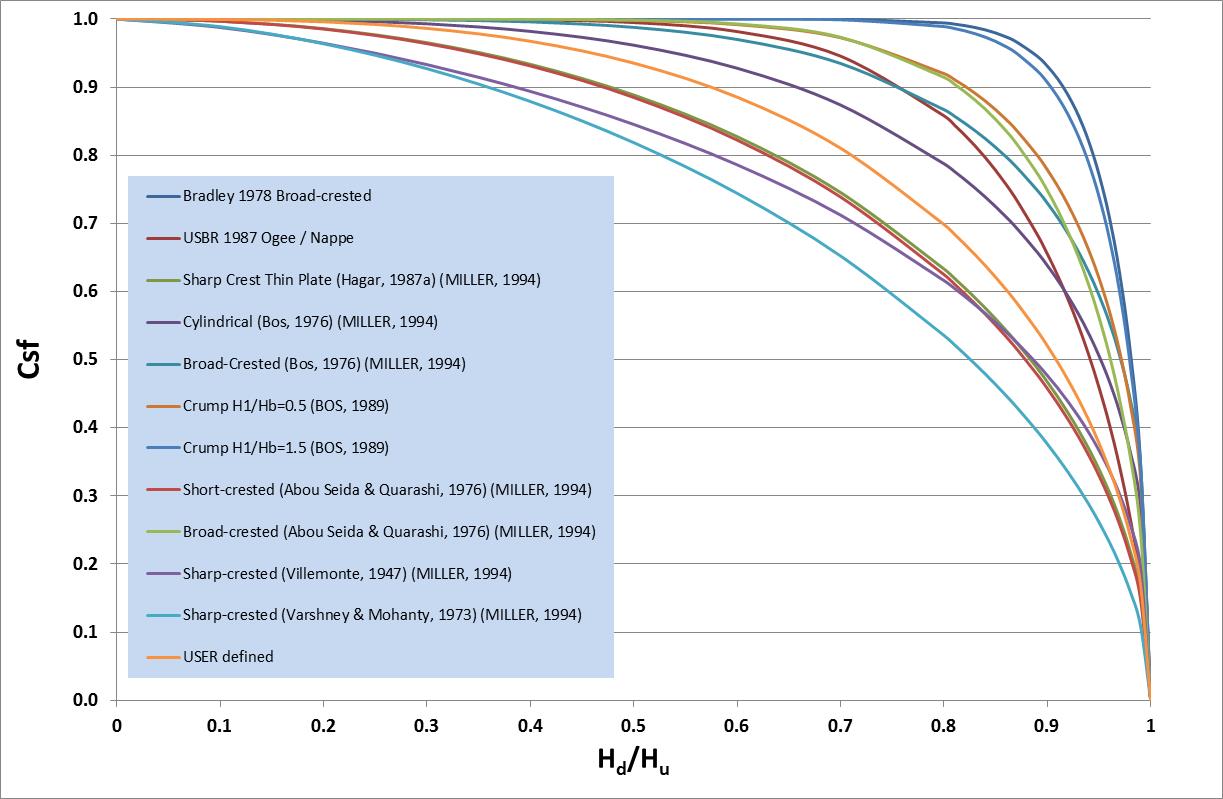
**Weir Submergence Curves using Villemonte Equation**

Figure 5.11: Weir Submergence Curves using Villemonte Equation

Table 5.17: Weirs: 1D Model Network (1d_nwk) Attribute Descriptions
No.  Default GIS Attribute Name Description Type
1 ID Unique identifier up to 12 characters in length. It may contain any character except for quotes and commas, and cannot be blank. As a general rule, spaces and special characters (e.g. “\”) should be avoided, although they are accepted. The same ID can be used for a channel and a node, but no two nodes and no two channels can have the same ID. Char(12)
2 Type The weir channel type as specified using the flags in Table 5.1 and 5.15. For example, a V-notch weir would be entered as “WV”. Char(4)
3 Ignore If a “T”, “t”, “Y” or “y” is specified, the object will be ignored (T for True and Y for Yes). Any other entry, including a blank field, will treat the object as active. Char(1)
4 UCS
(Use Channel Storage at nodes) 		If left blank or set to Yes (“Y” or “y”) or True (“T” or “t”), the storage based on the width of the channel over half the channel length is assigned to both of the two nodes connected to the channel. If set to No (“N” or “n”) or False (“F” or “f”), the channel width does not contribute to the node’s storage. See Section 5.12.1.1 for further discussion. Char(1)
5 Len_or_ANA The length of the weir channel, not the weir crest. Only used for automatically determining the storage at the nodes if the UCS attribute is set to “Y” or “T”. Not used in the conveyance calculations. If a no attribute is specified, the length of the digitised line is used. Float
6 n_nF_Cd Not used. Float
7 US_Invert

All Weir (excluding WO) Channel Types:
Sets the weir invert. Note that the invert is taken as the maximum of the US_Invert and the DS_Invert attributes. For W and WW weirs use -99999 to use the bed of the cross-section (if one exists) as the invert or weir crest.

WO Channel Type:
The absolute difference in height between the US_Invert and DS_Invert is used to set the height of the weir above its sill (usually denoted as P), which is used for recalculating the weir’s discharge coefficient each timestep. If the US_Invert and DS_Invert are the same value the primary upstream channel bed will be used to set the value of P. 		Float
8 DS_Invert See comments above for US_Invert. Float
9 Form_Loss Not used. Float
10 pBlockage

W Channel Type:
Not used. Reserved for future builds to fully or partially block W channels. The 1d_xs Skew attribute can be used to partially block cross-sections of these channels - see Table 5.4.

WB, WC, WD, WO, WR, and WS Channel Type:
The weir width is adjusted proportionally by the % blockage.

WT Channel Type:
The base width of the weir is adjusted proportionally by the % blockage.

WV Channel Type:
The V-notch angle is adjusted proportionally by the % blockage. 		Float
11 Inlet_Type Leave blank unless using the legacy MIKE 11 1D cross-section data feature. Char(256)
12 Conn_1D_2D Leave blank unless using the legacy MIKE 11 1D cross-section data feature, or if accessing a Flood Modeller cross-section database (.pro file), enter the label in the .pro file. Char(4)
13 Conn_No Leave blank unless using the legacy MIKE 11 1D cross-section data feature. Integer
14 Width_or_Dia

All Weir (excluding WT and WV) Channel Types:
The weir width in metres. The maximum of US_Invert and DS_Invert is used in conjunction with the Width_or_Dia attribute to define a rectangular section 5m (16.4ft) high. The automatic height given to the weir of 5m (16.4ft) so that the generation of node storage areas from channel widths are within a realistic range of elevations. Use Depth Limit Factor to allow water levels to exceed the 5m (16.4ft) range if required.

Note: For W and WW weirs if a cross-section for the channel exists, the cross-section profile will prevail over the automatic rectangular shape. Note: For operational weirs, the width of the weir when fully open.

WT Channel Type:
The width at the base of the trapezoidal weir. WT weirs are Cippoletti weirs that have side slopes of 1 horizontal to 4 vertical.

WV Channel Type:
Angle of the V-notch in degrees. Must be between 20º and 100º. 		Float
15 Height_or_WF

For non-operated weirs, this value can be used as a weir coefficient adjustment factor to be primarily used for model calibration or sensitivity testing. The weir coefficient is multiplied by this value. The resulting weir coefficient can be viewed in the .eof file and over time in the _TSL GIS layer. If zero or negative an adjustment factor of 1.0 (i.e. no adjustment) is applied.

For operational weirs, the height of the weir above the crest when fully up. 		Float
16 Number_of Not used. Integer
17 HConF_or_WC

W Channel Type:
Not used.

All Weir (excluding W) Channel Types:
Weir coefficient, Cd, in its dimensionless form. If less than or equal to zero the default value for the weir type in Table 5.16 is used.

Note that for WV weirs the default is to recalculate Cd every timestep. Entering a value greater than zero (0) will override this and apply a fixed Cd.

For WO weirs, the default is to recalculate Cd every timestep based on the actual head, while entering a value less than zero (0) will specify a design head for Cd calulation. Entering a value greater than zero (0) will apply a fixed Cd. Please see Section 5.7.4.3.1 for the detailed ogee crest weir approach.

For WD weirs the user must specify a non-zero positive value.

Note that published weir coefficients may be based on other non-dimensional or dimensional forms of the weir equation, and care should be taken in ensuring the coefficient is compatible with the form of the weir flow equation presented in Section 5.7.4.3. 		Float
18 WConF_or_WEx

W Channel Type:
Not used.

All Weir (excluding W) Channel Types:
Weir flow equation exponent Ex in the weir flow equation presented in Section 5.7.4.3. If less than or equal to zero the default value for the weir type in Table 5.16 is used. The default value is 1.5 for all weir types except for WV which is 2.5. 		Float
19 EntryC_or_WSa

W Channel Type:
Not used.

All Weir (excluding W) Channel Types:
Sets the submergence factor “a” exponent in the Villemonte Equation for calculating the weir submergence factor Csf (refer to equations in Section 5.7.4.3 and 5.7.4.4). If less than or equal to zero the default value for the weir type in Table 5.16 is used. 		Float
20 ExitC_or_WSb

W Channel Type:
Not used.

All Weir (excluding W) Channel Types:
Sets the submergence factor “b” exponent in the Villemonte Equation for calculating the weir submergence factor Csf (refer to equations in Section 5.7.4.3 and 5.7.4.4). If less than or equal to zero the default value for the weir type in Table 5.16 is used. 		Float

5.7.4.5 Automatically Created Weirs

Weirs representing overtopping of structures such as culverts and bridges may be automatically created without the need to digitise a separate line within a 1d_nwk layer. The structure must be digitised within a 1d_nwke layer (as opposed to a 1d_nwk layer) and a “W” specified alongside the original structure type. For example, to model a bridge and a weir representing overtopping of the road deck, specify type “BW”. The weir crest level and dimensions are specified within the additional attributes contained within a 1d_nwke layer and are explained in Table 5.18. The original W weir approach is adopted for calculating the flow (see Section 5.7.4.2).

The weir’s shape is assumed to be two rectangles on top of each other. The lower rectangle is reduced in width according to the percent blockage applied to the rail (i.e. the EN4 attribute in Table 5.18), and its height is the EN3 attribute. The upper rectangle is the full flow width and extends indefinitely in the vertical.

Alternatively, the flow over a structure can be manually digitised as a separate 1d_nwk weir channel parallel to the original bridge or culvert structure (i.e. the weir is connected to the ends of the bridge/culvert). Any of the available weir types can be used in this instance.

Table 5.18: 1D Model Network (1d_nwke) OPTIONAL Attribute Descriptions
No.  Default GIS Attribute Name Description Type
21 ES1 Not yet used (leave blank). Char(50)
22 ES2 Not yet used (leave blank). Char(50)
23 EN1 For BW, CW and RW channels, the flow width of weir (m or ft (if using Units == US Customary)) over the top of the B, C or R structure. If < 0.001, uses width multiplied by the number of culverts attribute for C and R channels. Float
24 EN2 For BW, CW and RW channels, the depth (m or ft (if using Units == US Customary)) of the bridge deck or culvert overlay. The weir level is set using the average of the upstream and downstream obverts plus the EN2 value. The level can be confirmed using the inverts_check file. Float
25 EN3 For BW, CW and RW channels, the depth of the hand rail (m or ft (if using Units == US Customary)). If < 0.001 assumes solid or no rail, depending on the EN4 attribute entry. Float
26 EN4 For BW, CW and RW channels, % blockage of the rail (e.g. 100 for solid rail, 50 for partially blocked, 0 for no rail). Float
27 EN5 For BW, CW and RW channels, the weir calibration factor. Is set to 1.0 if < 0.001 is specified. Float
28 EN6 Not yet used (leave as zero). Float
29 EN7 Not yet used (leave as zero). Float
30 EN8 Not yet used (leave as zero). Float

5.7.4.6 VW Channels (Variable Geometry Weir)

The VW (variable weir) channel allows the modeller to vary the cross-section geometry of a W weir over time using a trapezoidal shape. To set up a VW channel follow the steps below.

In the 1d_nwk layer, the following attributes are required:

  • ID = ID of the channel;
  • Type = “VW”;
  • Len_or_ANA = Nominal length in m (only used for calculating nodal storage if UCS is on);
  • US_Invert = -99999 (the invert level is specified in the .csv file discussed below);
  • DS_Invert = -99999 (the invert level is specified in the .csv file discussed below);
  • Inlet_Type = relative path to a .csv file containing information on how the weir geometry varies; and
  • Height_Cont = Trigger Value (the upstream water level to trigger the start of the failure; upstream water level is determined as the higher water level of the upstream and downstream nodes).

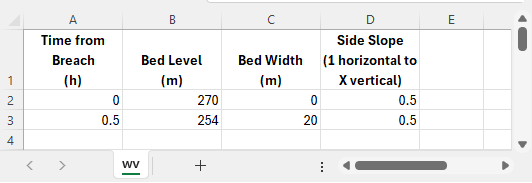
The .csv file must be structured as follows (also see example below):

  1. TUFLOW searches through the sheet until more than 4 numbers are found at the beginning of a row (Row 2 in the example below).
  2. Each row of values is read until the end of the file or a row with no or less than four numbers is found. There is no limit on the number of rows of data.
  3. The four columns must be as follows and in this order. The labels for the columns are optional.
    1. Time from start of breach in hours.
    2. Weir bed level in metres.
    3. Weir bed width in metres.
    4. Side slope (enter as the vertical distance in metres for one metre horizontal). For example, a value of 0.5 means a slope of two horizontal to one vertical.

In the example below, the weir once triggered will erode from a bed level of 270m to 254m, widen from a bed width of 0 to 20m and the side slope will remain constant at 0.5. The period of time for the erosion is 0.5hours.

Although in most cases the weir is eroded, the weir can also be raised/accreted as well or a combination of the two. Simply enter the change over time using as many rows as needed.

The original W weir approach is adopted for calculating the flow (see Section 5.7.4.2).

5.7.5 Spillways (SP)

Spillways (‘SP’) were introduced for the TUFLOW 2013-12 release and may also be used in operational mode as a gated spillway (see Section 5.9). Spillways may also be simulated and operated as Q or QO channels where the user provides the stage discharge relationships (see Section 5.8.2 and Section 5.9.3). The 1d_nwk attributes are presented in Table 5.19.

Spillways use the same equation as for advanced weirs (Section 5.7.4.3). For ungated spillways (i.e. SP, non-operated spillways) the same parameters as for Ogee Weirs are the default (see Table 5.16), except for Cd, which is fixed with the default value of 0.75. For Ogee Weirs, Cd is recalculated every timestep (see Section 5.7.4.3.1). The 1d_nwk attributes in Table 5.16 can be used to modify the flow equation parameters for SP channels in a similar manner for advanced weirs.

SPO channels also use the same equation when the gate is not affecting the flow (for more information on SPO channels refer to Section 5.9.6).

SP and SPO channels can also drown out as per the submergence curves for advanced weirs.

A working example of a model containing a spillway is provided in the 1D Structures Example Model Dataset on the TUFLOW Wiki.

5.7.6 Sluice Gates (SG)

For sluice gates refer to Section 5.9.5. The same approach applies as for SGO operated gates, except that the gate is assumed to be in a fixed position based on the 1d_nwk Height_or_WF attribute value. The 1d_nwk attributes are presented in Table 5.19.

5.7.7 Adjustment of Contraction and Expansion Losses

The energy losses associated with the contraction and expansion of flow lines into and out of a structure, can be automatically adjusted according to the approach and departure velocities in the upstream and downstream channels. This is particularly important where:

  • There is no change in velocity magnitude and direction as water flows through a structure. In this situation, there is effectively no entrance (contraction) or exit (expansion) losses and the losses need to be reduced to zero. Examples are:
    • A clear spanning bridge over a stormwater channel where there are no losses due to any obstruction to flow until the bridge deck becomes surcharged.
    • Flow from one pipe to another where the pipe size remains unchanged and there is no significant bend or change in grade.
  • There is a change in velocity, but the change does not warrant application of the full entrance and exit loss. This is the most common case where the application of the full entrance and exit loss coefficients (typically 0.5 and 1.0) will overestimate the energy loss through the structure. The full values are only representative of the situation where the approach and departure velocities are close to zero, for example, a culvert discharging from a lake into another lake where the velocity transitions from still water to fast flowing and to still water.

The entrance and exit losses are adjusted according to the equations below to take into account the change in velocity caused by the structure. The first equation is empirical, while the second equation to adjust exit losses can be derived from first principles.

\[\begin{equation} \text{C}_{\text{entrance_adjusted}} = \text{C}_{\text{entrance}}\left\lbrack 1 - \frac{\text{V}_{\text{approach}}}{\text{V}_{\text{structure}}} \right\rbrack \tag{5.14} \end{equation}\]

\[\begin{equation} \text{C}_{\text{exit_adjusted}} = \text{C}_{\text{exit}}\left\lbrack 1 - \frac{\text{V}_{\text{departure}}}{\text{V}_{\text{structure}}} \right\rbrack^{2} \tag{5.15} \end{equation}\]

Where:

  • V = Velocity (m/s or ft/s if using Units == US Customary)
  • C = Energy Loss Coefficient

As the structure velocity approaches the incoming and/or outgoing velocities, the loss coefficient approaches zero. When the incoming and/or outgoing velocity approaches zero (i.e. water is leaving/entering a large body of water), the loss coefficients approach their full value.

Tullis & Robinson (2008) provide an excellent proof for the need to adjust losses for different flow regimes using the exit loss equation above. The paper benchmarks different exit loss equations used within the industry methods against experimental flume test results.

The adjustment of losses feature is available to structures that require entrance and exit loss coefficients, namely culverts and bridges. For culverts, the adjusted entrance loss coefficient only applies where the flow is not inlet controlled (i.e. Regimes C, D, E, F, H and J in Table 5.6), and the adjusted exit loss is only influential where the flow is downstream controlled (i.e. Regimes D, F, H and J (subcritical at exit) in Table 5.6). For bridges, the application varies as discussed below.

If Structure Losses == ADJUST EXCEPT BG TABLES (default), the adjustment of the losses is only applied to culverts and B bridges with automatically generated loss tables using the 1d_nwk Form_Loss attribute (see Table 5.11). There is no adjustment for B bridges with a user specified BG or LC energy loss table, because bridge energy losses are most often based on coefficients from publications such as “Hydraulics of Bridge Waterways” (Bradley, 1978) or “Guide to Bridge Technology Part 8, Hydraulic Design of Waterway Structures” (Austroads, 2018) that have already taken into account the effects of contraction and expansion.

For BB bridges, the LC table should only represent the pier and submerged deck losses (see Section 5.7.4.4), as the adjustment of entrance and exit losses every timestep as per the equations above is always applied irrespective of the Structure Losses setting. The equations above conform with the approach for determining contraction and expansion losses in publications such as Hydraulics of Bridge Waterways.

For B bridges and culverts, if Structure Losses is set to “ADJUST”, or “A” has been specified in the 1d_nwk Type attribute (e.g. BA, CA, IA or RA), the entrance and exit losses are adjusted according to the equations above. For B bridges, because the entrance and exit losses are combined as one loss coefficient, the entrance and exit loss components are proportioned one-third / two-thirds respectively when applying the above equations. For the new BB bridge, entrance and exit losses are always adjusted as per the equations above and the Structure Losses setting is not relevant (also see Section 5.7.4.4).

The selection of the upstream and downstream channels on which to base the approach and departure velocities is as follows:

  • The upstream channel is determined as the channel which has a positive flow direction into the structure whose invert is closest to that of the upstream invert of the structure. If no channel exists, no adjustment of losses is made (this includes structures connected to a 2D domain). Note that the upstream channel must be digitised so that it has the same positive flow direction to that of the structure.
  • The downstream channel is selected on a similar basis to that for the upstream channel.
  • The selected upstream and downstream channels are listed in the .eof file for cross-checking (search for “Primary Channel”).
  • X channels can be used to connect additional channels and ensure that these are not considered the primary channel.

TUFLOW has no requirement of a minimum loss coefficient value for stability, and allows the adjusted coefficient to approach zero allowing this feature to correctly model the structure losses when the structure causes no disturbance to flow, or when one pipe discharges into another of identical size, grade and alignment.

The adjustment of loss coefficients does not apply to:

  • Any bend or additional loss for a culvert entered using the Form_Loss attribute in the 1d_nwk layer. This coefficient can be used to apply additional losses (e.g. pit or bend losses) that are not affected by changes in the relativity of the approach/departure and structure velocities.
  • Any additional loss coefficient component for BB bridges entered using the Form_Loss attribute in the 1d_nwk layer. This coefficient can be used to apply additional losses (e.g. pier losses) that are not affected by changes in the relativity of the approach/departure and structure velocities.
  • The ends of culverts and bridges that are connected to 2D SX or HX cells as the approach or departure velocity needs to be derived in some manner from the 2D velocity field. It is important not to be duplicating energy losses by applying exit losses to a 1D structure and simulating the same energy losses due to the flow expansion in the 2D domain – for further information see the Modelling Energy Losses at Structures AWS Webinar.

If Structure Losses is set to FIX, or “F” has been specified in the 1d_nwk Type attribute (e.g. BF, CF, IF or RF), the loss coefficients for B bridges and culverts are not adjusted. Fixing the entrance and exit losses for BB bridges is not available – use a B bridge instead.

The variation in time of the loss coefficients can be viewed using the _TSL output layer (see Section 15.2.4) or charted in the QGIS TUFLOW Viewer plugin.

If there is a manhole at the culvert end, a manhole energy loss approach (see Section 5.10.4) is used instead of the culvert’s contraction/expansion loss, and the above description does not apply.